Common Probability Distributions
확률 분포 관련에서 검색하다 해당 글을 찾았다. 분포 간의 관계를 잘 설명해놓은 거 같아 정리해봤다.
컴퓨터 사이언스에서 데이터 구조처럼 확률 분포는 통계의 중요한 기반이다. R이나 scikit-learn을 사용하면서 분포에 대한 이해없이 간단한 분석을 진행할 수 있지만, 결국에는 확률 분포를 이해하고 알맞은 분포를 선택하는 일이 필요하다.
수 백개의 확률 분포 중 가장 대표적이가 자주 사용되는 15개의 분포에 대해서 설명하겠다.
확률 분포
주사위를 굴려서 나오는 수나, 내일 날씨, 버스의 도착 시간 등은 결과가 나타나기 전까지는 어떤 일이 나올 지 모른다. 이렇게 변하는 값을 갖는 것을 변수라 한다. 이러한 변수의 값이 나타나기 전에는 어떤 값이 어느 정도로 잘 나오는 지 예측하는 수 밖에 없다. 이렇게 각 변수값이 나오는 정도와 매핑한 변수를 확률 변수라고 한다. 그리고 확률 분포는 확률 변수의 모든 값과 그에 대응하는 확률값들이 어떻게 분포되어 있는 지 나타낸 것이다. 각각의 분포들은 다른 모양을 갖고 있지만 한가지 큰 공통점을 갖는다: 분포 내 모든 확률값의 합은 1이다.
예를 들어, 동전을 던진다고 했을 때, 앞면 혹은 뒷면 값을 가진다. 동전을 던지기 전에 앞면가 나올 값은 둘 중 하나이기에 0.5 확률로 예측할 수 있다. 뒷면의 경우도 마찬가지다. 이러한 결과값들이 나오는 분포를 베르누이 분포라고 한다.
각기 다른 이름에도 불구하고 대표적인 분포들은 직관적이고 흥미로운 방법들로 연관되어 있으며, 그렇기에 기억하기도 쉽다. 아래 이미지는 15개의 분포들의 관계를 보여준다.
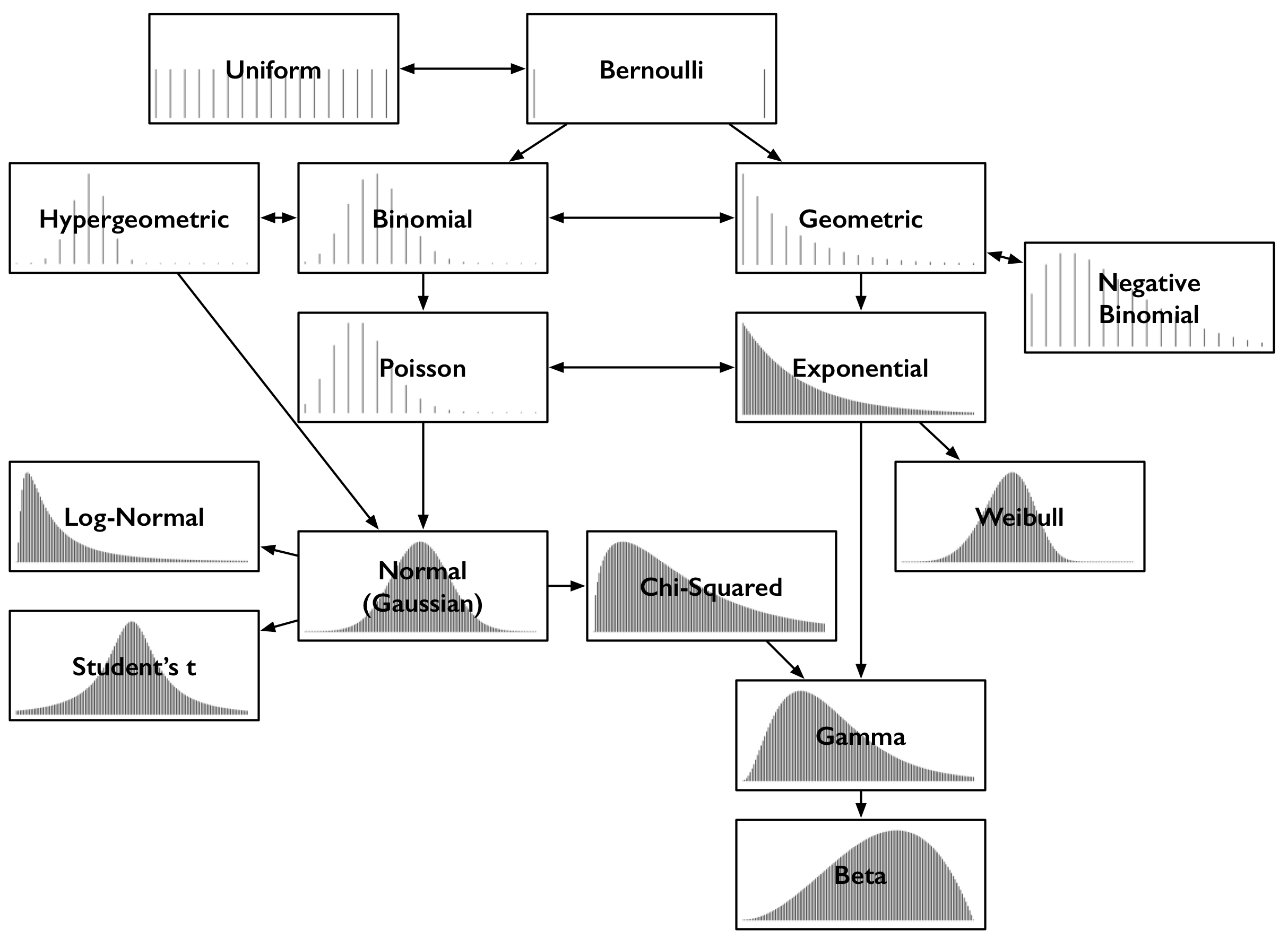
Common probability distributions and some key relationships
각 박스의 x는 가능한 모든 경우의 수를 나타내고, y는 해당 값의 확률을 나타낸다.각 확률값들의 간격이 큰 분포는 이산적이고 긔 외는 연속적이다.
Bernoulli and Uniform
균등분포는 모든 경우에 대해 확률값이 같은 분포를 의미한다. 확률값이 같은 주사위를 던지는 것이 균등 분포의 대표적인 예이다.
베르느이 분포는 결과값이 1이거나 0인 두가지의 경우에서만 다룬다. 위 동전 던지기의 예시가 베르누이 분포를 따른다고 할 수 있다. 물론 1이나 0이 나올 확률은 균등하지 않아도 된다.
Binomial and Hypergeometric
이항 분포(Binomial)은 베르누이 분포 결과값의 합으로 생각할 수 있다. 만약 동전을 20번 던진다면, 앞면이 몇 번 나올까? 이러한 결과값은 이항 분포를 따른다. \(n\)번 동전을 던지고 앞면(성공)이 나올 확률을 \(p\)라 하자. 각 시행은 베르누이를 따른다. 또 각각의 시행은 전이나 후의 시행에 영향을 미치지 않으므로 독립적이다.
검은 공과 하얀 공이 담겨있는 상자에서 공을 여러번 뽑는 것도 마찬가지다. 매번 공을 뽑고 다시 상자에 넣는다면 검은 공은 몇 번 나올까? 와 같은 문제는 모두 이항 분포를 따른다.
반대로 공을 뽑고 다시 상자에 넣지 않는다고 해보자. 그렇다면 다시 검은 공 혹은 하얀 공을 뽑을 확률은 달라지게 된다. \(n\)개 중에서 비복원 추출 방법으로 \(k\)개가 뽑힐 확률은 초기하분포(Hypergeometric)을 따른다.
Poisson
고객 센터에서 매 분마다 오는 고객 전화 수는 어떤 분포를 따를까? 고객 전화가 오는가(1), 오지 않는가(0)만 봤을 때는 이항 분포를 따르는 거 같다. 하지만 같은 1초에 2번의 전화만 올 수도 있고, 수백 번의 전화가 올 수도 있다. 초를 더 작은 단위인 60,000 millisecond로 나누어 더 많은 시행과 각 전화 1통에 대한 확률로 본다고 해도 베르누이 분포를 따르지 않는다. 하지만 시행을 무한대로 한다면 타당한 결과가 나온다. \(n\)(시간)을 무한대로하고 확률 p가 0이 되도록하여 np값이 똑같도록 만든다. 이는 마치 매우 작은 무한한 시간 조각에서 전화 올 확률이 무한히 작은 시행을 무한히 하는 것과 같다. 이를 푸아송 분포(Poisson)라고 한다.
이항 분포와 같이 푸아송 분포는 사건이 일어난 횟수에 관한 분포이다. 사건의 확률 p와 사건 횟수 n 대신에 상수값 np를 나타내는 평균 비율 \(\lambda\)를 사용한다. 푸아송 분포는 사건이 일어날 비율이 주어졌을 때, 특정 시간 내에 사건 횟수를 구하는 방법인 상황에서 쓰인다.
Geometric and Negative Binomial
베르누이 분포에서 또 다른 분포가 나온다. 처음으로 동전 앞면이 나오기 전까지 몇 번의 뒷면이 나오는가? 동전 뒷면이 나오는 개수는 기하 분포(Geometric)를 따른다. 베르누이 분포와 같이 성공 확률 \(p\) 파라미터를 가진다. 하지만 전체 시행의 횟수 파라미터 n은 사용되지 않는다. 왜냐하면 실패한 시행 횟수 자체가 결과값이기 때문이다.
이항 분포가 “몇 번의 성공을 했는가?”이라면, 기하 분포는 “첫 성공 전에 몇 번의 실패를 했는가”라고 볼 수 있다.
음이항분포(Negative binomial)은 간단한 일반화다. \(r\)번의 성공이 일어나기 전에 몇 번의 실패를 했는가이다. 물론 \(r\)이 1이면 기하 분포이기 때문에 음이항분포에서는 \(r\)이 1이 아니다. 음이항분포는 또 반대로 \(r\)번의 실패 전에 몇 번의 성공을 했는 지 나타낼 때도 있다.
이항 분포와 초기하 분포가 비슷하듯이 음이항 분포와 기하 분포도 비슷한 쌍이다.
Exponential and Weibull
다시 고객 센터 예를 생각해보자: 다음 고객 전화가 오기까지 얼마나 걸릴까? 매 초마다 전화가 오지 않으면 실패이고 올 때까지의 시간이므로 기하 분포를 따를 거 같아 보인다. 실패한 시행 횟수는 아무도 전화하지 않은 시간(매 초)을 나타내기에 다음 전화까지 대기 시간과 비슷하지만 정확히는 다르다. 기하 분포를 따르는 시행의 합은 언제나 온전한 초 단위로 얻어지지만, 고객 전화가 오게되는 마지막 초 이하 단위 값은 구하지 못한다.(8.5초만에 전화가 왔을 때 0.5초를 구하지 못함)
푸아송 분포를 구했던 것과 같이 기하 분포를 무한히 작은 시간 조각으로 나누면 지수 분포(Exponential)를 얻을 수 있다. 지수 분포는 연속형이기에 전화가 오기까지의 정확한 시간을 설명해줄 수 있다. 지수 분포 역시 \(\lambda\) 파라미터를 가진다.
푸아송의 “매 시간 얼마나 많은 사건”은 지수 분포의 “사건까지의 얼마나 많은 시간”과 연관이 있다. 매 시간마다 일어나는 사건 수는 푸아송 분포를 따른다면, 각 사건간의 시간은 지수 분포를 따르며 같은 비율 \(\lambda\)를 사용한다. 두 분포의 이러한 관계는 둘 중 하나를 얘기할 때 나오므로 중요하다.
“사건까지의 시간” 혹은 “실패까지의 시간”을 얘기할 때면 지수 분포가 떠올라야한다. 이러한 개념은 매우 중요하여 실패까지의 시간을 설명하는 일반적인 분포들이 더 존재한다. Weibull 분포 역시 그 중 하나이다. 지수 분포는 사건이 일어나는 비율이 상수일 때 적합하지만, weibull 분포는 사건에 대한 비율이 증가하거나 감소할때도 나타낼 수 있다.
실패까지의 시간에 관한 거라면 Weibull을 떠올려야 한다.
Normal, Log-Normal, Student’s t, and Chi-squared
정규 분포(Normal or Gaussian)은 아마 가장 중요한 분포이다. 어느 분포에서 표본을 여러 개 가져와 합한다고 하자. 그 합의 분포는 대략 정규 분포를 따르게 된다. 더 많은 수를 합하게 된다면, 그 합의 분포는 더 정규 분포에 가까워진다(물론 이상치나 결측치가 없는 분포에서 독립적으로 추출되어야 한다). 이를 중심 극한 정리라고 한다.
이러한 의미에서 정규 분포는 모든 분포와 연관되어 있다. 하지만 사건들의 합의 분포들에서만 특히 관련되어 있다. 베르누이 시행의 합은 이항 분포를 따르고, 이 시행 횟수가 커질수록 이항 분포는 더 정규 분포에 가까워진다. 이항 분포의 사촌뻘인 초기하 분포 역시 이러한 특성을 가진다. 이항 분포의 극한인 푸아송 분포 역시 비율 파라미터가 커질수록 정규분포에 가까워진다.
로그 정규 분포를 따르는 결과는 로그를 취한 값이 정규 분포를 따르는 특성을 가진다. 혹은 정규 분포의 지수값이 로그 정규 분포하다고도 할 수 있다. 만약 사건들의 합이 정규하게 분포해 있다면, 사건들의 곱들은 로그 정규 분포를 따른다.
스튜던트 t-분포는 t-검정을 위해 다른 과학 분야의 많은 비통계학자들이 배운다. 정규 분포의 모평균 값을 추론할 때 사용되고, 또 파라미터 값이 커질 때 정규분포에 가까워진다. t-분포의 특징은 정규 분포보다 꼬리 부분이 더 두껍다는 것이다.
기네스는 stout를 더 잘 만들기 위해 100년 넘게 통계를 사용했다. William Sealy Gosset(고셋)은 더 좋은 보리를 키우기 위해 새로운 통계 모델을 개발했다. 고셋은 다른 양조업자들이 이 아이디어를 이해시키기 위해 게재를 허락 받았고, “Student”라는 가명으로 출판한다. 고셋의 t를 따와 t-분포라 불리운다.
마지막으로 카이제곱(Chi-squared) 분포이다. 이는 정규 분포 값의 제곱을 합한 값의 분포이다. 편차의 제곱합에 기반한 카이제곱 검증을 뒷받침하는 분포이다.
Gamma and Beta
감마(Gamma) 분포는 지수 분포와 카이제곱 분포의 일반화된 모형이다. 지수 분포처럼 더 복잡한 대기 시간에 관한 모델이다. 예를 들어, 감마 분포는 다음 \(n\)개의 사건이 일어나기까지의 시간을 모델링할 수 있다. 머신 러닝에서 다른 분포의 켤레 사전 분포(conjugate prior)로 자주 등장한다.
베타(Beta) 분포 역시 다른 많은 분포의 켤레 사전 분포이다. 데이터 사이언티스트의 관점에서는 이것이 감마 분포를 만든 목적이다.

Leave a comment